|
´X¦ó¥ú¾Ç´N¬O¥Î¥ú½u³o¤@°²·Qªº´X¦ó½u¨Ó³B²z¡B¸ÑÄÀ¡B¬ã¨s¥úªº©Ê½è(¦p¡G¶Ç¼½¡B¤Ï®g¡B§é®gµ¥)ªº¾Ç¬ì¡C´X¦ó¥ú¾Ç¿í´`¥H¤U´XÓ°ò¥»ì²z¤Î©w«ß¡G
(1)
¥ú½uªºª½½u¶Ç¼½(«ß)¡C
(2)
¥ú§ô¦U³¡¤À¬Û¤¬¿W¥ß(¿W¥ß«ß)¡C
(3)
¥úªº¤Ï®g«ß¡C
(4)
¥úªº§é®g«ß¡C
(5)
¥úµ{¥i°f©Ê¡C
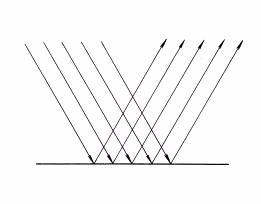
¥ú¦b¬Y¤@¤¶½è¤¤¶Ç¼½¡A·í¹J¨ì¥t¤@ºØ¤¶½èªºªí±®É¡A·|µo¥Í¥H¤U¤TºØ±¡ªp¡G
(1)
¥úªº¤Ï®g(reflection of light)¡@·í¥ú½u¦æ¶i¦Ü¨â¤¶½èªº¬É±¤W®É¡A³¡¤À¥ú½u¥Ñ¬É±ªð¦^ì¬É½è¤¤¡A¦ý¦æ¶i¤è¦Vµo¥Í¤FÅܤơA³o¤@²{¶HºÙ¤§¬°¥úªº¤Ï®g¡C
(2)
¥úªº§é®g(refraction of light)¡@·í¥ú½u¦æ¶i¦Ü¨âºØ¤¶½èªº¬É±¤W®É¡A¸g¬É±¶i¤J¥t¤@¤¶½è¤¤¡A¦¹®É¥ú½uªº¦æ¶i³t«×µo¥Í¤FÅܤơA¦P®É¶Ç¼½¤è¦V¤]µo¥Í¤F§ïÅÜ¡A¦¹ºØ²{¶HºÙ¤§¬°¥úªº§é®g©Î©}¥ú¡C
(3)
¥úªº§l¦¬(absorption of light)¡@·í¥ú½u»Pª«Åé¬Û¹J®É¡A´Nn¦³¤@³¡¤À¥ú½u³Q§l¦¬¡A¦ÓÂà¤Æ¦¨¬°¨ä¥L¯à¶q§Î¦¡¡A¦p¼ö¯àµ¥¡C¨ä§l¦¬¤§¦h¤Ö¡A«hµøª«Åéªí±¤Î¨ä²Õ¦¨¸Óª«Å骺ª«½èµ²ºc¦Ó©w¡C
(¤@)
¥úªº¤Ï®g
1.
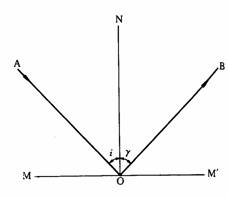
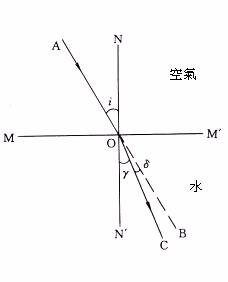
¥úªº¤Ï®g©w«ß¡@¤U±§Ú̬ݤ@¬Ý¥ú½u¦b¤¶±(MM')¤Wµo¥Í¤Ï®gªº³W«ß(¹Ï1-13)¡A¨ä¤¤AO¬°¤J®g½u(incident ray)¡AO¬°¤J®gÂI(point
of incidence)¡ANO¬°³q¹L¤J®gÂI¨Ã»P¸ÓÂI¬É±¬Û««ª½ªº½uºÙ¬°ªk½u(normal)¡AOB¬°¤Ï®g½u(reflected
ray)¡A¤J®g½u»Pªk½u¶¡ªº§¨¨¤¬°¤J®g¨¤(angle of incidence)¡A¥Î¢ñªí¥Ü¡F¤Ï®g½u»Pªk½u¶¡ªº§¨¨¤¬°¤Ï®g¨¤(angle of reflection)¡A¥Î¢úªí¥Ü¡C
¥úªº¤Ï®g©w«ß¡G(1)¤J®g½u¡B¤Ï®g½u©Mªk½u¤TªÌ©~¦P¤@¥±¡A¤J®g½u»P¤Ï®g½u¤À©~ªk½u¨â°¼¡F(2)¤J®g¨¤µ¥©ó¤Ï®g¨¤¡C
2.
±Ã誺¤Ï®g¤Î¨ä¦¨¹³¡@¯àµo¥Í¤Ï®gªº¥ú·Æ¬É±ºÙ¬°±Ãè¡A±Ãè¤À¬°¥±Ãè¤Î²y±Ãè(¥Y²y±Ãè¤Î¥W²y±Ãè)¡C
(1)
¥±Ã誺¤Ï®g¤Î¨ä¦¨¹³ ¯àµo¥Í¤Ï®gªº¥ú·Æ¥±ºÙ¬°¥±Ãè(plane
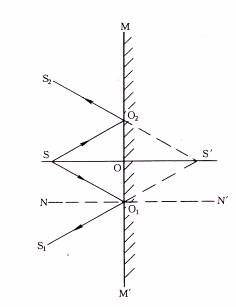
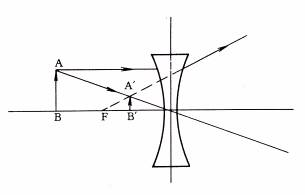
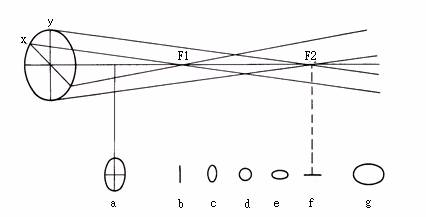
mirror)¡C®Ú¾Ú¥úªº¤Ï®g©w«ß¡A¥i¥H¨D¥Xµo¥úÂI©Îª«Åé¦b¥±Ãè¸Ìªº¹³(¹Ï1-14)¡C³]¤@ÂI¥ú·½S¦ì©ó¥±ÃèMM'¤§«e¡A¥ú½uSO1¤ÎSO2¤À§O¬°ÂI¥ú·½µo¥Xªº¨â±ø¤J®g¥ú½u¡A¸gO1¤ÎO2¨â¤J®gÂI«á¤Ï®g¡A¤À§O¬°OlSl¤ÎO2S2¨â±ø¤Ï®g¥ú½u¡A¦¹¨â±ø¤Ï®g¥ú½u¬°µo´²¥ú§ô¡A·í¨ä®g¤J²´¤º®É¡A±N·Pı¨ä¦p¦P¦bOlS1¤ÎO2S2¨â¬Û¤Ï©µ½u¤§¥æÂIS'³Bµo¥X¡CS»PS'»PÃ豫«ª½¬Û¥æ©óOÂI¡A®Ú¾Ú¤Ï®g©w«ß¤Î¤T¨¤§ÎSOO1»PS'OOl¬°¥þµ¥¤T¨¤§Î¡A¬GSOµ¥©óOS'¡A§Yª«¶Z»P¹³¶Z¬Ûµ¥¡A»PÃè±MM'¬Û¹ïºÙ¡AS'¬°µê¹³¡A¦]¹ê»Ú¥ú½u¨Ã¥¼±qS'µo¥X¡A¦Ó¬O²´¤º©Ò±µ¨üªº¥ú½u»PS'©Òµo¥X¥ú½uªº¤è¦V¬O¤@Pªº¡C¥Ñ¦¹¥i¶i¤@¨B±À¾É¥X½u¬qªº¦¨¹³¡B±ªº¦¨¹³¤Î¥ßÅ馨¹³¡C
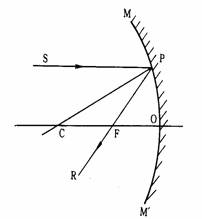
¦b¹Ï1-15¤¤¡AMM'¬°¤@¥W²y±Ãè¡FC¬°¥W²y±Ã誺¦±²v¤¤¤ß(¤]ºÙ¬°¥ú¾Ç¤¤¤ß)¡FCO¬°¥D¶b¡FF¬°µJÂI¡FO¬°²y±Ã誺³»ÂI¡C
¦p¡G¦³¤@§ô¥¦æ¥úSPªu¥D¶bCO¤è¦V§ë®g¨ì¥W²y±Ãè¤W¡A¸g¤Ï®g«á§Î¦¨¤Ï®g½uPR¡A·|¶°¦b¥D¶b¤Wªº¤@ÂIF¡A¦¹µJÂI¬°¹ê©ÊµJÂI¡C
¦Ó¸g¥Y²y±ÃèMM'¤Ï®g«áªº¥ú½u§¡´²¶}¡Aªu¤Ï®g¥ú¤§¤Ï¤è¦V©µªø¥æ©ó¤@ÂIF¡A¦¹µJÂI¬°µê©ÊµJÂI¡C¨£¹Ï1-16¡C
①
¥Î²y±Ã覨¹³¤½¦¡¡A¨D¥X¹³ªº¤j¤p¡B¤è¦V»Pµê¹ê
1¡þu+1¡þv¡þ=1¡þf=2¡þr
¨ä¤¤¡Au¬°ª«¶Z¡Av¬°¹³¶Z¡Af¬°µJ¶Z¡Ar¬°¦±²v¥b®|¡C¦b¦¹¤£½×¥W(©Î¥Y)±Ãè¡A¦ì©óÃè±³»ÂI¤§¥ª¬°t¡A¥k¬°¥¿¡C§Y¡Gª«¶ZªºË¼Æ»P¹³¶Z˼Ƥ§©Mµ¥©óµJ¶ZªºË¼Æ¡A©Î2¿¦±²v¥b®|ªºË¼Æ¡C¦P®ÉÁÙ¥i¥H¬Ý¥X¡G1¡þf=2¡þr
¡÷
r=2f
¡÷
f=r¡þ2¡C
©ñ¤j²v¡G§Y¬°¹³ªøy'»Pª«ªøyªº¤ñÈ¡C
m=
y'¡þy
®Ú¾Ú¬Û¦ü¤T¨¤§Îªº¬Û¹ïÀ³Ã䦨¤ñ¨Ò¡A«h¥i±o¥X
y'¡þy=
v¡þu
¦b¥ú¾Ç¤W³W©w¡A¥Ñ¶b¦V¤W´ú©w¬°¥¿¡A¦V¤U´ú©w¬°t¡A¬G¦b½T©w¹³ªº¤è¦V(¥¿¥ß¡BË¥ß)®É¡A«h
y'¡þy= -v¡þu
②
¥Î§@¹Ïªk¨D¥X¹³ªº¦ì¸m¡B¤j¤p¡Bµê¹ê©MË¥¿¡C
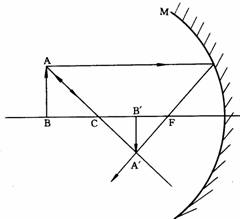
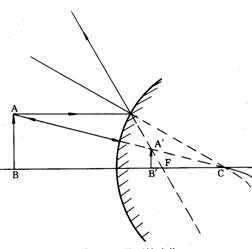
A.»P¥D¶b¥¦æªº¤J®g¥ú½u¸g¤Ï®g«á¥²¸g¥DµJÂI¡F
B.¹LµJÂIªº¤J®g¥ú½u¤Ï®g«á¥²¥¦æ©ó¥D¶b¡F
C.³q¹L¥ú¾Ç¤¤¤ß(¦±²v¤¤¤ß)ªº¤J®g½u¨ì¹FÃ豫á¡A¨ä¤Ï®g¥ú½u¥²ªuì¸ôªð¦^(§Y¦ì©ó¦Pª½½u¤W¡A¤è¦V¬Û¤Ï)¡F
D.¦V¤Ï®gÃè³»ÂI¤J®gªº¥ú½u¡A¥²¨Ì¥D¶b¬°ªk½u¡A«ö¤J®g¨¤µ¥©ó¤Ï®g¨¤ªº¤Ï®g¤è¦V¦Ó¤Ï®g¡C
¥H¤W¥|±ø¤Ï®g¥ú½u¤¤¡A¥ô¿ï¨â±ø(±`¥ÎA©MC)§Y¥i¨D¥X¬Y¤@ª«ÂI¹³ªº¦ì¸m¡C¹Ï1-17¤Î¹Ï1-18¬°¥Î§@¹Ïªk¤À§O¨D¥X¥W±Ãè¤Î¥Y±Ã誺¦¨¹³¹Lµ{¡C
¥W±Ã誺¦¨¹³¡AÀHª«Åé©Ò³Bªº¦ì¸m¤£¦P¡A¨ä¤j¤p¡Bµê¹ê¤ÎË¥¿§¡¤£¦P¡F¥Y±Ã誺¦¨¹³¡A§¡¬°ª½¥ßÁY¤pªºµê¹³¡Aª«Åé¶ZÃ豶V»·¨ä¹³¶V¤p¡C
(¤G)
¥úªº§é®g(©}¥ú)
·í¥ú½u¹J¨ì¨âºØ¤£¦P¤¶½èªº¬É±®É¡A°£¤@³¡¤À¥ú½u³Q¤Ï®g¦^줶½è¤¤(µo¥Í¤Ï®g)¥~¡AÁÙ¦³¤@³¡¤À¥ú½u«h¶i¤J¥t¤@ºØ¤¶½è¤¤¡A³o³¡¤À¥ú½u±Nµo¥Í¤@©wµ{«×ªº¥ú¦æ¶i¤è¦Vªº§ïÅÜ(Âà§é)¡A³oºØ¥úªº°¾§é²{¶HºÙ¬°¥úªº§é®g©Î©}¥ú(1ight refraction)¡C
1.
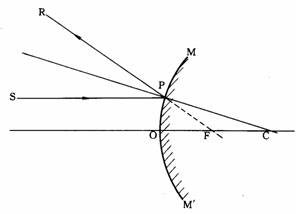
¥ú¦b¥±¤Wªº§é®g¡@·í¥ú¥Ñ¤@ºØ¤¶½è®g¦V¥t¤@ºØ¤¶½èªº¬É±¬°¤@¥±®Éªº§é®g²{¶H¡A¨£¹Ï1-19¡C
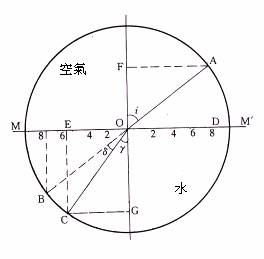
Á|¨Ò¡G(¹Ï1-20)¤¤³]¦³¤@¥ú½uAO®g¦VªÅ®ð»P¤ô¥æ¬ÉªºMM'¤¶±¤W¡A¦b¶i¤J¤ô¤¤«áªuOC¤è¦V¶Ç¼½¡A§@¤@Ó¥b®|¬°1ªº³æ¦ì¶ê¡A¨ä¤¤AO¬°¤J®g½u¡AFG¬°ªk½u¡AOC¬°§é®g½u¡Ai¬°¤J®g¨¤¡Ar¬°§é®g¨¤¡A£_¬°°¾±×¨¤¡C
ºÙ¬°¸Ó¤¶½èªºµ´¹ï§é®g²v©ÎºÙ¬°§é®g²v¡C¥ú¦b¯uªÅ¤¤¤£¨ü¥ô¦óªý¤O¡A¦Ó³q¹LªÅ®ð®É²¤¨üªýê¡A¥ú½u¥Ñ¯uªÅ¶i¤JªÅ®ð¤¤®É¡A¨ä§é®g²v¬°1.00029¡A¦¹È»P¯uªÅȬۮt¬Æ·L¡A¦]¦¹¦b²´¬ì¾Ç¤¤¡A§Ú̱NªÅ®ð»P¯uªÅ·í§@¦P¤@¤¶½è¬Ý«Ý¡A²´©}¥úª«½èªº§é®g²v§¡«ü¹ïªÅ®ð¦Ó¨¥ªº§é®g²v¡A¦p¡G¨¤½¤¬°1.376¡A´¹Å鬰1.4085µ¥¡C
§é®g²v¸û¤pªº¤¶½èºÙ¬°¥ú²¨½è¡A¦Ó§é®g²v¸û¤jªº¤¶½èºÙ¬°¥ú±K½è¡C
②
¬Û¹ï§é®g²v(relative index of refraction)¡@¦p²Ä¤@ºØ¤¶½èªºµ´¹ï§é®g²v¬°n1¡A¦Ó²Ä¤GºØ¤¶½èªºµ´¹ï§é®g²v¬°n2¡A¥ú¥Ñ²Ä¤@¤¶½è¶i¤J²Ä¤G¤¶½èªº§é®g²v¬°n21¡A§Y²Ä¤GºØ¤¶½è¹ï²Ä¤@ºØ¤¶½èªº¬Û¹ï§é®g²v¬°
n21=n2¡þn1
¨Ò¦p¡G¥ú½u¥Ñ¤ô¶i¤J¤ô´¹®É¡A¨ä¤ô´¹¹ï¤ôªº¬Û¹ï§é®g²v¬°
n21=n2¡þn1=1.55¡þ1.33=1.17
·í¥ú½u¦Û¥ú²¨½è®g¤J¥ú±K½è®É§é®g½u°¾¦Vªk½u(ªñªk½u)¡F¦Ó¥Ñ¥ú±K½è®g¤J¥ú²¨½è®É¡A§é®g½u«h»·Â÷ªk½u¡C
¯S§O´£¥Xªº¬O¡A¥ú¥Ñ¤@ºØ¤¶½è¶i¤J¥t¤@ºØ¤¶½èªº§é®g²v¡A¤£¶È©M³o¨âºØ¤¶½èªº©Ê½è¦³Ãö¡A¦P®ÉÁÙ»P¤J®g¥úªºªiªø(¥úªºÃC¦â)¦³Ãö¡C¦p¡G¤ô¹ï¬õ¦â¥úªº§é®g²v¬°1.329¡A¦Ó¹ïµµ¦â¥úªº§é®g²v¬°1.344¡C¤¶½èªº§é®g²vÀH¥ú¦âªº¤£¦P¦Ó¦³¤£¦P¼ÆȪº³oºØ²{¶H¡AºÙ¬°¥úªº¦â´²²{¶H(chromatic dispersion)¡C¦b²´¬ì©}¥úÀˬd¤¤ªº¨â¦âªk¹êÅç©Î¦â¹³®t¹êÅç(chromatic
test)´N¬OÀ³¥Î³o¤@²{¶H¤Îì²z¦Ó³]pªº¡C
2.
¤TÙ±Ã誺§é®g
(1)
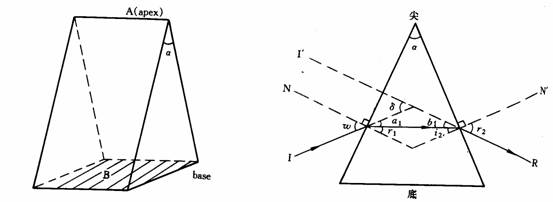
¤TÙ±Ã誺ºc¦¨¡@¤TÙ±Ãè(prism)¬O¥Ñ³z©úª«½è(¦p¬Á¼þ)ºc¦¨ªº¤@Ó¤TÙ±¬WÅé(¹Ï1-21)¡C¥¦¥Ñ¤Ó±²Õ¦¨¡A»PÙ±Ãä««ª½ªººI±ºÙ¬°Ù±Ã誺¥DºI±(¹Ï1-22)¡A§e¤T¨¤§Î¡C¤TÙ±Ãè¨â¥ú¾Ç±ªº§¨¨¤ºÙ¬°¦y(apex)©Î³»¨¤(§Y£\¨¤)¡A¹ïµÛ¦yªº±ºÙ¬°©³(base)¡A¥Ñ¤TÙ±Ãè³»©Î¦yªº¤¤¤ß¨ì©³±¤¤¤ßªºª½½u¬°©³¦y½u¡C¤J®g¥ú½u»P¸g¤TÙ±Ãè§é®g«áªº§é®g¥ú½u¤§¶¡ªº§¨¨¤ºÙ¬°°¾¦V¨¤(angle of deviation)¡A§Y£_¨¤¡C
(2)
¤TÙ±Ã誺¥ú¾Ç©Ê½è
①
ª«¹³²¾¦ì¡G¦p¹Ï1-22©Ò¥Ü¡A¤J®g¥ú½u¢×§ë¦V¤TÙ±Ã誺¤@Ó¥ú¾Ç±¤W«áµo¥Í§é®g¡A¦]¬°¬O¥Ñ¥ú²¨½è¶i¤J¥ú±K½è¡A¦]¦Ó§é®g«á¾aªñªk½u¡A¦Ó·í¤TÙ±Ã褺ªº§é®g½u¹J¨ì¥t¤@Ó¥ú¾Ç±¤W®É¡A«hµo¥Í²Ä¤G¦¸§é®g¡A³o¦¸§é®g«o¬O¥Ñ¥ú±K½è¶i¤J¥ú²¨½è¡A¦]¦Ó§é®g»·Â÷ªk½u¡A¦Ó¦V¤TÙ±Ã誺°ò©³¤è¦V°¾§é¡C·í§Ú̳q¹L¤TÙ±ÃèÆ[¹î¨Ó¦Û¤J®g½u¤è¦V¢×ªº¤@Óª«Åé®É¡A«h·Pıª«Åé¦ì©óªu§é®g½u¢à©µ¦ù½u¢×'ªº¤è¦V¡C°¾¦V¨¤«×£_=a1+b1¸g±À¾É£_=i1+r2-£\¡A§Y°¾¦V¨¤¬°¤J®g¨¤»P§é®g¨¤¤§©M´î¥h¤TÙ±Ã誺³»¨¤¡C¦]¦¹¡A¥ú½u³q¹L¤TÙ±Ãè«á¦V°ò©³°¾§é¡A¦V¦yºÝ§ë®g¡A§Y³q¹L¤TÙ±ÃèÆ[¹îª«Åé®É¡A¥²Ä±¤TÙ±Ãè«á¤èªºª«Åé¦V¤TÙ±Ã誺³»¨¤¤è¦V²¾¦ì(¹Ï1-23)¡C
¦b²´¬ìÁ{§É¤W¡A±`À³¥Î³o¤@ì²z¶i¦æ½ÆµøªºÁB¥¿¡BÁô±×ªº´ú¶q¤Î±×µøªºÀˬd»P°V½mµ¥¡C
②
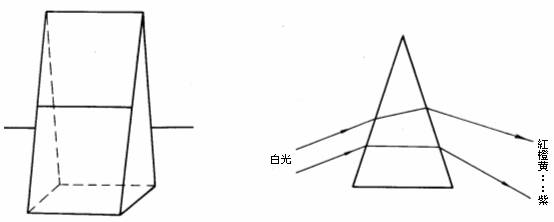
¦â´²§@¥Î(chromatic dispersion)¡G¸g¹L¤TÙ±Ã誺¥Õ¦â¥ú¦b¸g¾ú¤F¨â¦¸§é®g«á³Q¤À¸Ñ¦Ó²£¥Í¬õ¡B¾í¡B¶À¡Bºñ¡B«C¡BÂÅ¡Bµµªº³sÄò¥úÃСA³oºØ²{¶HºÙ¬°¤TÙ±Ã誺¦â´²§@¥Î©ÎºÙ¤À¥ú§@¥Î§Y¥úªº¤À¸Ñ¡C³o¬O¥Ñ©óÙ±Ã誺¤¶½è¹ï¤£¦Pªiªøªº¥ú½u¨ã¦³¤£¦Pªº§é®g²v¡A¦]¦¹¡A¤£¦Pªiªø(ÃC¦â)ªº¥ú¡AÁöµM¤J®g¨¤¬Û¦P¡A¦ý¦Uªiªøªº¥ú¦U«ö¨ä©T¦³ªº§é®g¨¤§é®g¡A©ó¬O®g¥Xªº¥ú½u«öªiªø(ÃC¦â)¤ÀÂ÷¶}¡C¦]¦¹¡A¤TÙ±Ãè¤]³QºÙ¬°¦â´²Ù±Ãè¡C©}¥ú¤¶½èªº§é®g²v¬OÀHªiªøªº¼W¥[¦Ó´î¤Öªº¡A¦]¦¹¡A¦â´²Ù±Ãè¨Ï¥i¨£¥ú¤¤ªºµµ¦â¥ú°¾§é³Ì¤j¡A¬õ¦â¥ú°¾§é³Ì¤p(¹Ï1-24)¡C
(3)
¤TÙ±Ã誺ªí¥Üªk
①
¤TÙ±Ã誺©}¥ú¤O³æ¦ì
¢¹.³»¨¤©w«×ªk¡G®Ú¾Ú¤TÙ±Ãè³»¨¤¨¤«×ªº¤j¤p¦Ó½T©w¨ä©}¥ú¤Oªº±j®z¡C¦p¡G³»¨¤¬°5o¡A«hºÙ¬°5o¤TÙ±Ãè¡C¦]¦¹ªk¥¼¦Ò¼{¤TÙ±Ãèºc¦¨§÷®Æ¹ï¥úªº§é®g²v¡A©Ò¥H¹ê¥Î»ùȤ£¤j¡C
¹Ï1-23 ¤TÙ±Ã誫¹³²¾¦ì²{¶H
¹Ï1-24 ¤TÙ±Ã誺¦â´²§@¥Î
¢».»p¤óªk(Prentice)¡G¬°°ê»Ú¼Ð·Ç¤TÙ±Ãè³æ¦ì¡A¥Ø«e²´¬ì±`¨Ï¥Î¦¹³æ¦ì¡A¨ä©w¸q¬°¡G³q¹L¤TÙ±ÃèÆ[¹î1¦Ì³Bªºª«Åé¡A¦pª«Åé¦VÙ±Ãè¦yºÝ²¾¦ìlÍù¦Ì¡A«hºÙ¬°1Ó¤TÙ±Ãè«×¡A¥Î²Å¸¹¡µªí¥Ü¡A§Y1¡µ¡C¦b²´¬ìÁ{§É¤¤¡A±`¥Îªº¤TÙ±Ã觡¦b20¡µ¥H¤º¡A¨f¤óªk¤Î»p¤óªk¬Û®t¬Æ·L¡C
②
¤TÙ±Ã誺¦ì¸m¡G¤TÙ±Ãè±`¥H¨ä©³¦y½uªº¤è¦V¨Óªí¥Ü¨ä¦ì¸m¡A¦b²´¬ìÁ{§É¤¤¡A®Ú¾Ú¤£¦P±¡ªp¡A¥i±N¤TÙ±Ã誺©³¦y½u¸m©ó¥ô¦ó¤è¦V¤W¡A¦]¦¹¨ä¦ì¸m»P¬WÃ誺ªí¹F§¹¥þ¬Û¦P¡C
3.
³æ¤@²y±ªº§é®g¡@²´·ú¬O¤@ӥѦh²y±¤ÎY¤z§é®g²v¤£¦Pªº³z©ú¤¶½è©Òºc¦¨ªº©}¥ú¨t²Î¡A¬°¤F§ó¦n¦a¬ã¨s²´ªº©}¥ú¨t²Î¡A§ÚÌ¥ý¬Ý¤@¬Ý¥ú½u¦b³æ¤@²y±¤Wµo¥Íªº§é®g²{¶H¡C
(1)
¹Ï1-25 ³æ¤@²y±§é®g¦¨¹³
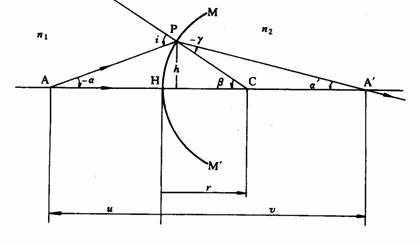
¤£ÅÜ¡A§Y¦ì©ó¥D¶b¤W¡FAP¬°¥t¤@±ø¤J®g½u¡A¨ì¹F¬É±PÂI®Éµo¥Í§é®g¡A®Ú¾Ú§é®g©w«ßµo¥Í°¾§é¡A»P¥D¶b¬Û¥æ©óA'¡AA'¬°Aªº¶µÂI¡AAH¬°ª«¶Z(u)¡AHA¡¦¬°¹³¶Z(v)¡A¦pªG§Ú̶Ȭã¨sªñ¶b¥ú½u¡A¨º麽©Ò¦³ªº¨¤³£«Ü¤p¡Asin ¡@i Áͪñ©ói¡A®Ú¾Ú§é®g©w«ß¥i¥H²¼g¬°nli = n2r¡A¤SPÂI¶Z¥D¶bªº¶ZÂ÷¬°H¡A«h
£\=h/u,
£\¡¦=h/v,
£]=h/r
¡îr=£]-£\¡¦,
i=£]+ (-£\)
¡ïn1 (£]-£\)=
n2(£]-£\¡¦)
n1 (h/r -
h/u) =
n2(h/r -
h/v)
n2/v -
n1/u = (n2 -
n1)/
r
³o¤@¤½¦¡§Y¬°³æ¤@²y±ªñ¶b¥ú½u¦¨¹³ªº°ò¥»ªí¹F¦¡¡C
¦b¦¹¦¨¹³¤½¦¡¤¤À³ª`·N²Å¸¹³W«h¡G
¢¹.©Ò¦³¤ô¥¶ZÂ÷§¡¦Û¬É±³»ÂI°_¶i¦æ´ú¶q¡A¦pª«¶Zu¬°±qH¦VA¶i¦æ´ú¶q¡A¥ô¦ó»P¤J®g½u¤è¦V¤@Pªº¶ZÂ÷§¡¬°¥¿È(¦pr,v)¡A¤è¦V¬Û¤Ï¬°tÈ(¦pu)¡F
¢º.»P¥D¶b««ª½ªºª«»P¹³ªº¶ZÂ÷(§Y««ª½¶ZÂ÷)¡G§¡¦Û¥D¶b¬°ìÂIºâ°_¡A¦V¤WªÌ¬°¥¿È¡A¦V¤UªÌ¬°tÈ¡C
¢».¤J®g¨¤»P§é®g¨¤§¡¦Ûªk½u¶q°_¡A°f®É°w¬°¥¿È¡A¶¶®É°w¬°tÈ¡C
¢¼.¥ú½u»P¥D¶bªº§¨¨¤¦Û¥ú½u¶q¦Ü¥D¶b¡A°f®É°w¬°¥¿È¡A¶¶®É°w¬°tÈ¡C
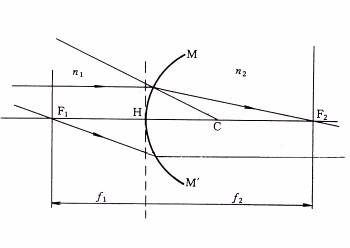
¥Ñ©óª«¶Z¦ì©óµL»·³B(§YµL½a¤j)¡A¬G¡An1/u=0¡A¦¹®É
f2=v¡A«h
n2 /
f2 = (n2 -
n1) /
r
¦P¼Ë¦b²Ä¡Ð¤¶½è¤¤ªº¥D¶b¤W¥²¦³¤@ÂIF¡A¸g¹L¸ÓÂIªº¤J®g¥ú½u¡A¨ì¹F²y±¤¶±¤W¡A³q¹L§é®g«á¥ú½u¥¦æ©ó¥D¶b¡C¸ÓÂI§Y¬°²Ä¤@¥DµJÂI(«e¥DµJÂI)¡A§é®g²y±³»ÂI¦Ü¸ÓÂIªº¶ZÂ÷
f 1 ¬°²Ä¤@µJ¶Z¡C
¦¹®É¥Ñ©ó¹³¶Z¬°µL»·³B¡An2 /
v=0¡Aª«¶Z¬°
f1¡A
-n1¡þf1=(n2-n1)¡þr
¦]¦¹¡A²y±ªº©}¥ú¤OD¬°
D=(n2¡Ðn1)¡þr =
n2¡þf2 = -n1¡þf1
¨ä¤¤r,
f1¤Îf2§¡¥H¦Ì¬°³æ¦ì®É¡A©}¥ú¤Oªº³æ¦ì¬°©}¥ú«×¡C
(3)
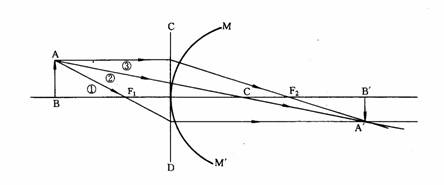
´X¦ó§@¹Ïªk¡@¨£¹Ï1-27¡A³]¦³¤@ª«ÅéAB¦ì©ó¥D¶b¤W¡A¸g³æ¤@²y±§é®g¦Ü²Ä¤GºØ¤¶½è¤¤¡A¦b¦¹¥Î§@¹Ïªk¨D¥X¨ä¦b²Ä¤G¤¶½è¤¤©Ò§Î¦¨ªº¹³¡C
Aª«ÂIªº¹³A'¡A¥i¥H³q¹L¥H¤U¤T±ø¥ú½u¤¤¥ô·N¤G±ø¥ú½uªº¥æÂI©Ò½T©w¡C
¢¹.³q¹L²Ä¤@¥DµJÂIFlªº¥ú½u¡A¸g¥D¥±CD§é®g«á»P¥D¶b¥¦æ¡F
¢º.³q¹L²y¤ß(µ²ÂI)Cªº¥ú½u¡A¦]««ª½¤J®g¬G¸g§é®g«á¤è¦V¤£ÅÜ(¦]¬°ªk½u§¡¸g¹L¦¹ÂI)¡F
¢».»P¥D¶b¥¦æªº¥ú½u¡A¸g¥D¥±§é®g«á³q¹L²Ä¤GµJÂIF2¡C
4.
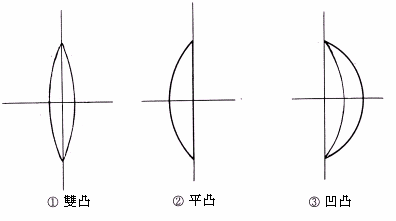
³zÃ誺§é®g¡@³zÃè(lens)¬O¥Ñ¬Á¼þ©Î¨ä¥L³z©úª«½è©Ò»s¦¨¡A¨ä¤¤¦Ü¤Ö¦³¤@Ó±¬O²y±¡A¨ä¯SÂI¬O¥i¥H¨Ï¥ú½u¦¨µJ¡C³zÃè¤À¬°²y±³zÃè(²yÃè)©M¶ê¬W±³zÃè(¬WÃè)¨âºØ¡C
(1)
¹Ï1-28 ²y±³zÃ誺§Î¦¨
¦]¦¹¡A²y±³zÃè¤W¦U®|½uªºÅs¦±«×¬Û¦P¡A¨ä¦U®|½uªº©}¥ú¤O¬Ûµ¥¡C²y±³zÃè¤S¤À¬°¥Y¡B¥W²y±³zÃè¡A®Ú¾Ú²y±³zÃè¨â±§Îª¬ªº¤£¦P²Õ¦X¡A¨CºØ²yÃè¤S¤À¬°¤TºØ¡C
¥Y²yÃè¤À¬°¡G1Âù¥Y²yÃè¡A2¥¥Y²yÃè¡A3¥W¥Y²yÃè¡C¨£¹Ï1-29¡C
¥W²yÃè¤À¬°¡G1Âù¥W²yÃè¡A2¥¥W²yÃè¡A3¥Y¥W²yÃè¡C¨£¹Ï1-30¡C
¥H¤W¤»ºØ²yÃè¤ÀÃþ¡A¨ä«á±ªº¦r¨M©wµÛÃ誺©Ê½è¡A¥Y³zÃ褤¶¡«p¨âÃäÁ¡¡A¥W³zÃ褤¶¡Á¡¨âÃä«p¡C
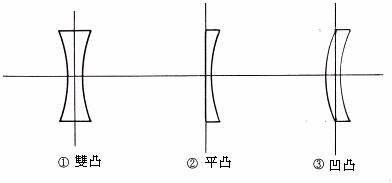
A.
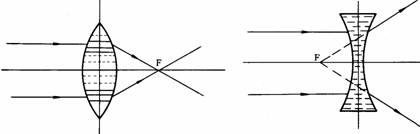
¥Y²y±³zÃè(convex spherical lens)¡G¦¹ºØ³zÃè¬Û·í©ó¥Ñ³\¦h°ò©³¦V¤¤¤ßªº¤TÙ±Ãè©Ò²Õ¦¨(¹Ï1-31)¡C¥¦æ¥ú½u¸g¥Y²yÃè§é®g«á¦V¤¤¤ß¶°¦X§Î¦¨µJÂI¡C¥Y³zÃè¥Î¡§¡Ï¡¨ªí¥Ü¡C
B.
¥W²y±³zÃè(concave spherical lens)¡G¥¦¬Û·í©ó¥Ñ«Ü¦h¦yºÝ¦V¤¤¤ßªº¤TÙ±Ãè©Ò²Õ¦¨(¹Ï1-32)¡C¥¦æ¥ú½u¸g¥W²yÃè«á¥ú½u´²¶}¡A¤£¯àµ²¦¨¹ê©ÊµJÂI¡Aªu´²¶}¥ú½u¦V«á©µªø¡A¥iµ²¬°µêµJÂI¡C¥W³zÃè¥Î¡§¡Ð¡¨ªí¥Ü¡C
①
²y±³zÃ誺©}¥ú¤O¡G³zÃ誺§é¥ú¯à¤O¥Î©}¥ú«×(diopter¡AD)¨Óªí¥Ü¡A¦p¥¦æ¥ú½u¸g¬Y¤@³zÃè«á¦bÂ÷³zÃè1m»·³B»EµJ¡A«h¸Ó³zÃ誺©}¥ú¤O¬°¤@Ó©}¥ú«×(1D¡Adiopter)¡C¦p¦b2m³B¦¨µJ«h¬°0.5D¡C¦p¥Îf¥NªíµJ¶Z¡A«h³zÃ誺©}¥ú¤O(©}¥ú«×)=1¡þ¥DµJ¶Z(m)¡A§YD=1¡þf¡A¨ä¤¤¢î¥H¦Ì¬°³æ¦ì¡C¥Y³zÃ誺©}¥ú«×¥Nªí¶°¦X¥úªº¯à¤O¡A¥W³zÃè¥Nªí¹ï¥úªº´²¶}¯à¤O¡C
³zÃè©}¥ú¤Oªº¤j¤pÁÙ¨ú¨M©ó³zÃ誫½è¹ï¥úªº§é®g²v¡B³zÃèªí±ªºÅs¦±«×¤Î³zÃè©Ò³B¤¶½èªº±¡ªp(§Y³zÃè©P³ò¤¶½èªº§é®g²v±¡ªp)¡C
¸m©óªÅ®ð¤¤ªº²y±³zÃè¨ä¨âÓ±ªº©}¥ú¤O¡ADl¡BD2¤À§O¬°
Dl=(n¡Ð1)¡þr1=(n¡Ð1)Rl
D2=(1¡Ðn)¡þr2=
¡Ð(n¡Ð1)¡þr2=
¡Ð(n1¡Ð1)R2
¦]¬°R=1¡þr¡FR¬°²y±¦±²v¡Ar¬°²y±¦±²v¥b®|¡C
¦p¬°Á¡³zÃè¡A«h¨äÁ`©}¥ú¤O¬°¨â±©}¥ú¤O¤§©M¡C
D=Dl+D2=(n-1)(1¡þr1¡Ð1¡þr2)=(n¡Ð1)(Rl¡ÐR2)Æ¢
②
²y±³zÃ誺¦¨¹³
A.
¦¨¹³¤½¦¡
³zÃ覨¹³ªº¤@¯ë¤½¦¡¡G1¡þu
+ 1¡þv=1¡þf
¦b¦¹¡AµL½×¥Y³zÃèÁÙ¬O¥W³zÃè¡A¹êª«¤Î¹ê¹³ªº¶ZÂ÷¥Î¥¿¸¹¡§+¡¨¡Fµêª«¤Îµê¹³ªº¶ZÂ÷¥Ît¸¹¡§¡Ð¡¨¡F¥Y³zÃ誺µJ¶Z¬°f¡A¥W³zÃ誺µJ¶Z¬°¡Ðf¡C
B.
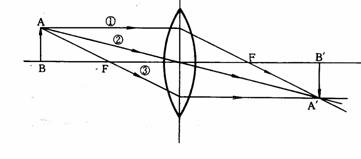
§@¹Ïªk¦¨¹³ì«h
¬Y¤@ª«ÂI¡A¸g¤@²y±³zÃè¦Ó¦¨¹³¡A¨º麽¸Óª«ÂI©Òµo¥Xªº¥ú½u¤¤¡G
a.
»P¥D¥ú¶b¥¦æªº¥ú½u¡A¸g§é®g«á¡A¹L¥DµJÂI¡F
b.
¸g¹L¥ú¾Ç¤¤¤ß(µ²ÂI)ªº¥ú½u¤è¦V¤£ÅÜ¡F
c.
¸g²Ä¤@¥DµJÂIªº¥ú½u¡A¸g§é®g«á¥¦æ©ó¥D¥ú¶b¡C
¦b¥H¤W³o¤T±ø½u¤¤¥ô¨ú¨â±ø½uªº¥æÂI§Y¬°³o¤@ª«ÂIªº¹³ÂI¡A¨Ì¦¹¥i¥H¨D¥X¾ãÓª«Å骺¹³¡C
¹Ï1-33¤Î¹Ï1-34¤À§O¬°¥Y³zÃè¤Î¥W³zÃ誺¦¨¹³¹Lµ{¡C
¥Y³zÃè©Ò¦¨ªº¹³¡A«h®Ú¾Úª«Åé©Ò¦b¦ì¸m¤£¦P¦Ó¦U²§¡C
a.
ª«Åé¦ì©óµJÂI¥~¡A¬°Ë¥ßªº¹ê¹³¡F
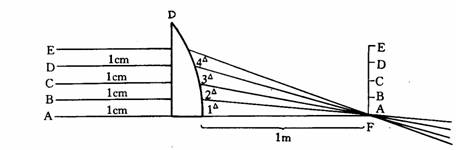
Ù±Ãè¤O¡C¦]¦¹¡A¥i¥H¬Ý¥X¶V¾a©PÃ䳡¨ä³zÃ誺ٱÃè¤O¶V±j¡C¦P®É³zÃè«×¼Æ·U°ª¡A¨ä¤TÙ±Ãè®ÄÀ³¥ç¶V¤j¡C³zÃè¤W¬YÂIªº¤TÙ±Ãè®ÄÀ³P¡µµ¥©ó³zÃ誺©}¥ú«×¢Ò»P¶Z¥ú¾Ç¤¤¤ßªº¶ZÂ÷d (¥HÍù¦Ì¬°³æ¦ì)ªº¼¿n¡A§YPrentice¤½¦¡
P¡µ
=
d¡ED
¦p©}¥ú«×¬°1Dªº¥Y³zÃè¡A¶Z¥ú¾Ç¤¤¤ß 4cm ³Bªº¤TÙ±Ãè®ÄÀ³¬°
P¡µ= 4
¡Ñ 1= 4¡µ
¦]¦¹¦b°tÃè®É¡AÀ³±j½Õ¥ú¾Ç¤¤¤ß»Pµø¶bªº«¦X¡A¥H§K²£¥Í¤TÙ±Ãè®ÄÀ³¡A¨ÏÀ¹Ãè«á¥X²{²´¯h³Ò¤Î±m¦âÃ䪺·Pı¡C
(2)
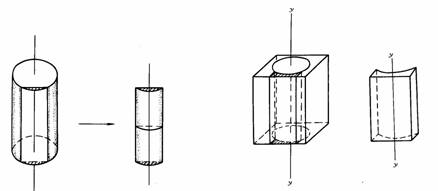
¬W±³zÃè(cylinder lens)¡@¬W±³zÃè(²ºÙ¬°¬WÃè)¬O±q¶ê¬W§Îªº©}¥ú¤¶½è¹êÅé¤WÁa¤Á¤U¨Óªº¤@³¡¤À(¹Ï1-36)¡C©Î¦p¦P¶ì¦¨¶ê¬WÅ骺¥~¼Ò«¬ªº¤@³¡¤À(¹Ï1-37)¡C
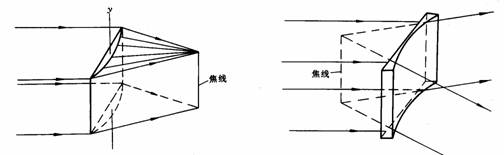
¨äå±»P¶ê¬WÅé¶byªº¤è¦V¤@P¡A¦]¦¹¬WÃ誺¶b»P¶ê¬WÅé¶b¤è¦V¬Û¦P¡A¥Ñ©ó¬WÃè¦b¶bªº¤è¦V¤W¤£¬O¦±±¡A©Ò¥Hªu¬WÃè¶b¤è¦V¤J®gªº¥ú½u¡A¤£µo¥Í¥úªº©}§é¡F¦Ó»P¶b««ª½ªº¤è¦V¡A¨äªí±¬°¦±±¡A©Ò¥Hªu¦¹¤è¦V¤J®gªº¥ú½u¡A«hµo¥Í§é®g¡A¥Y±ªÌ¨Ï¥ú½u·|»E¡A¥W±ªÌ¨Ï¥ú½uµo´²¡C¥H¤W¥i¥H¬Ý¥X¬WÃè¶È¤@Ó¶b¦V¹ï¥ú½u¦³§é®g§@¥Î¡A¦]¦¹³q¹L¬WÃ誺¥ú½u¤£¬O§Î¦¨¤@ÓµJÂI¡A¦Ó¬O§Î¦¨¤@±øµJ½u(focal line)¡AµJ½uªº¤è¦V»P¶b¥¦æ(¹Ï1-38)©M(¹Ï1-39)¡C
¦b²´¬ìÁ{§É¤W¡A¬WÃè§Y¬°´²¥úÃè¤ù¡A¨ä¤¤§t¶bªº®|½uºÙ¬°®z¥D®|½u¡A§Y¶bªº¦ì¸m¡F»P¶bª½¥æªº®|½uºÙ¬°±j¥D®|½u¡A³q±`¥H±j¥D®|½uªº²y±©}¥ú¤Oªí¥Ü¬WÃ誺«×¼Æ¡C
(3)
¹Ï1-38 ¥Y¬WÃ誺©}¥ú§@¥Î¡@¡@¡@¡@¡@¡@¡@¡@¹Ï1-39 ¥W¬WÃ誺©}¥ú§@¥Î
¦b³o¤@©}¥ú¨t²Î¤¤¡Ax¬°¤ô¥¤l¤È½u¡A¨äÅs¦±«×¸û¤j¡Ay¬°««ª½¤l¤È½u¡AÅs¦±«×¸û¤p¡A·í¤@§ô¥¦æ¥ú½u¸g¹L³o¤@©}¥ú¨t²Î«á¡A¦]¤ô¥¤l¤È½uªº©}¥ú¤O¸û±j¡A¸g§é®g«á¥ý¦¨¥æ©ób
³B¡A¦¹®É««ª½¤l¤È½u¥Ñ©ó¨ä©}¥ú¤O¸û®zÁÙ¥¼¯à¦¨µJ¡A¦]¦Ó§Î¦¨¤@ÁY¤pªº««ª½µJ½u¡FµM«á¡A¤ô¥¥ú½uÄ~Äò¦V«e¦æ¦Ó´²¶}¡A¦Ó««ª½¥ú½u¤´¦b¶°¦X¹Lµ{¤¤¡A·í¤ô¥¥ú½uªº´²¶}¤O¶q»P««ª½¥ú½uªº¶°¦X¤O¶q¬Û·í®É§Yd
³B¡A«h§Î¦¨¤@ӫܤpªº¶ê§Î¥ú´³¡A¦¹¶ê§Î´³ºÙ¬°Sturm¥úÀ@¤¤ªº³Ì¤pÀ±´²´³¡F·í¥úÄ~Äò«e¦æ®É¡A««ª½¥ú½u«h¦b¢î³B§Î¦¨¤@¤ô¥ªºµJ½u¡Cb
»P
f¶¡ªº¶ZÂ÷¬°µJ¶¡¶Z¡A¦b¥H¤W¥ú¾Ç¶êÀ@¤¤¨S¦³¤@³B¯à§Î¦¨µJÂI¡A¬G©Ò§Î¦¨ªº¹³§¡¤£²M´·¡C
¦bÁ{§É¤W¡A½Æ©Ê´²¥úªº¦¨¹³»P¤Wz¦¨¹³¹Lµ{¬Û¦P¡A¦ý¦pµøºô½¤¦ì©ó¥H¤W¥úÀ@ªº¤£¦P¦ì¸m¤W¨ä©}¥ú©Ê½è¦³©Ò¤£¦P¡AYµøºô½¤¦ì©óa
³B¡A«h¬°½Æ©Ê»·µø´²¥ú¡F¦ì©ób
³B¬°³æ¯Â»·µø´²¥ú¡F¦ì©óf
³B¬°³æ¯Âªñµø´²¥ú¡F¦ì©óg
³B¬°½Æ©Êªñµø´²¥ú¡F¦ì©óµJ¶¡¶Z¤º¡A§Yb
»P¢î¤§¶¡¬°²V¦X©Ê´²¥ú¡C
¦b¥ú¾Ç¤¤¡A±N¨âÓ¥Dn¤l¤È½u¨ã¦³¤£¦PÅs¦±«×ªº¥ú¾Ç±ºÙ¬°½Æ¦±±©Î¦«¤O§J±¡A¨ä§Îª¬µS¦p¹ªªº°¼±¡C¦b°t»s²´Ãè®É¡A¥i¥H°µ¦¨¤@±¬°½Æ¦±±¡A¥t¤@±¬°²y±ªº³zÃè§Y½Æ¦±±³zÃè¡A¤]ºÙ¬°¦«¤O§JÃè¤ù(Toric lens)¡A¨äÀuÂI¬°¥i¥H®ø°£³zÃ誺¹³®t¡C
(¤T)
¦@¶b²y±¨t²Î
¦pªG¦b¬Y©}¥ú¨t²Î¤¤¡A§é®g²y±¤£¥u¤@Ó¡A¦Ó¬O¥Ñ¦hÓ²y±²Õ¦¨¡A¦Ó¥B³o¨Ç§é®g±ªº¦±²v¤¤¤ß¤S§¡¦b¤@±øª½½u¤W¡A¥¦©Òºc¦¨ªº©}¥ú¨t²Î§YºÙ¬°¦@¶b²y±¨t²Î¡A¨ä¤¤¡A³s±µ¦±²v¤¤¤ßªºª½½u§Y¬°¥D¥ú¶b¡C
¦b¦@¶b²y±©}¥ú¨t²Î¤¤¡A¥i¥ý¨D¥Xª«Åé³q¹L²Ä¤@Ó§é®g±ªº¹³v1¡AµM«á¦A¥Hv1§@¬°²Ä¤GÓ§é®g±ªºª«¡A¦A¨D¥X¨ä³q¹L²Ä¤GÓ§é®g±ªº¹³v2¡A¡K¡A¨Ì¦¹Ãþ±À¡Aª½¦Ü¨D¥X³q¹L³Ì«á¤@Ó(¢ö)§é®g±ªº¹³¬°¤î¡C³o¤@¤èªk¬°³v¦¸¦¨¹³ªk¡A¤SºÙ°l¥[ªk¡C¨ä¦¨¹³¤½¦¡¦p¤U¡G
n1/
v1
=
n/
u1+ (n1-n)/
r1
n2/
v2 =
n1/u2+ (n2-n1)/
r2„³n2/v2=n1/v1+(n2-n1)/r2
ú`
ú`
nn/vn
= (nn-1)/un+(nn-nn-1)/ Rn
³q¹L¥H¤W¤èµ{¦¡¡A³Ì«á§Y¥i¨D¥X¬Y¦@¶b²y±©}¥ú¨t²Î©Ò¦¨¹³ªº¦ì¸m¡C
¦b¹ê»ÚÀ³¥Î¤¤¡A³v¦¸¦¨¹³ªkpºâ°_¨Ó«Ü·Ðº¾¡A¦]¦¹±`¥H¨t²Îªº¤T¹ï°òÂI²¤Æ¨D¹³¡C
(¥|)
Á¡³zÃ誺Áp¦X
Á¡³zÃè¡G¬O«ü·í³zÃ誺«p«×«Ü¤p¡A»PµJ¶Z¬Û¤ñ¥i¥H©¿²¤¤£p®É§Y¬°Á¡³zÃè¡AÁ¡³zÃèÁp¦X¬ã¨sªº¬O¥Ñ¨âөΨâÓ¥H¤Wªº¦@¶bÁ¡³zÃè²Õ¦X¦Ó¦¨ªº¥ú¾Ç¨t²Îªº¦¨¹³¤Î¨ä©}¥ú°ÝÃD¡A¦b¦¹§Ú̶Ȭݤ@¬Ý¨âÓÁ¡³zÃ誺Áp¦X¡C
1.
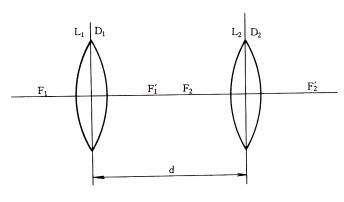
¨âÓÁ¡²y±³zÃ誺Áp¦X(¹Ï1-41) ³zÃèL1»PL2ªº©}¥ú«×¤À§O¬°Dl¤ÎD2¡A¨â³zÃ褧¶¡ªº¶ZÂ÷¬°d¡A«h¦¹¨t²Îªº©}¥ú«×D¬°
D=D1+D2
- dD1D2
D=D1+D2
¹Ï1-41¡@Á¡³zÃèÁp¦X
2.
¨âÓÁ¡¬W±³zÃ誺«Å|Áp¦X
(1)
Y¶b¦V¬Û¦PªºÁ¡¬WÃè«Å|¦b¤@°_(§Y¶b¦V¬Û¦PªºÁp¦X)¡A«hÁp¦X«áªº©}¥ú¤O¬°¨âªÌ©}¥ú¤Oªº¥N¼Æ©M¡A¦Ó¶b¤£ÅÜ¡C
C1 x
90o
Á|¨Ò¡G-3.00C x 10o
(2)
¶b¦V««ª½ªºÁp¦X¡@¦³¥H¤U¤TºØ±¡ªp¡G
①
¦P¸¹¦P¤O¥¿¥æ¡A«h¦¨¬°¦P¸¹¦P¤O²yÃè
+ C1 x
90o
¨Ò¦p¡G+1.50C x 90o
②
¦P¸¹¤£¦P¤O¥¿¥æ¡A«h¬°¤@Ó¦P¸¹²yÃè¡A«×¼Æ¬°¸û§CÃè¤ùªº©}¥ú«×¡F»P¤@Ó¦P¸¹¬WÃè¡A«×¼Æ¬°¨âÃè¤ù«×¼Æ¤§®t¡A¶b«h»P¸û°ªÃè¤ùªº¶b¤@P¡C
+C1
x 90o
¦p¡G+2.00 x 90o
③
¤Ï¸¹¦P¤O¥¿¥æ(§Y¡G¥æ¤e¬WÃè)¡A«h¬°¤@Ó²yÃè(«×¼Æ»P¨ä¤¤¤@Ó¬WÃè¤ùªº«×¼Æ¤Î²Å¸¹¬Û¦P)»P¤@Ó¬WÃè(«×¼Æ¬°¨â¬WÃè¤ù¤§©M¡A²Å¸¹»P²yÃè¬Û¤Ï¡A¶b¨ú¦P²Å¸¹ªº¶b)¡C
+C x 90o
¨Ò¦p¡G+2.00C x 90o
©Î¡Ð2.00S
(3)
¬WÃè±×¥æÁp¦X¡@§Y¨âÓ¬WÃè¬Û¥æ§Y¤£¬°0o¡A¤]¤£¬°ªº90o¥ô·N¨¤¡C
·í¨âÓ¬WÃèC1¡BC2ªº¶b¦¨¡Ð©w¨¤«×a®É¡AYÁp¦X«á¡A«öThompson¤½¦¡
«h
S= (C1+C2
- C) /2
sin2£r= C2sin2a / C
¨ä¤¤¡AC¬°¦X¦¨¬WÃ誺©}¥ú¤O¡AS¬°²yÃè©}¥ú¤O¡A£r¬°¦X¦¨¬WÃè»PClªº§¨¨¤¡C
(¤)
«p³zÃè
«p³zÃè¹ê½è¤W´N¬O¥Ñ¨âÓ²y±©Ò²Õ¦¨ªº¦@¶b²y±¨t²Î(homocentric system)¡A¨D¨ä¦¨¹³¥iÀ³¥Î¦@¶b²y±¨t²Î¨D¹³ªk¡A¹Lµ{«D±`Ácº¾¡A¦ýÀ³¥Î¦@¶b²y±¨t²Îªº°òÂI·§©À¥i¤j¤j¬Ù²¤¤§¡A¥B¥¦ÁÙ¾A¥Î©ó©Ò¦³¦@¶b¨t²Î¡C
1.
¦@¶b¨t²Îªº¤T¹ï°òÂI
(1)
¹Ïl-42¡@¦@¶b¨t²Îªº¤T¹ï°òÂI
(2)
¨â¥DÂI¡@³q¹LF1ªº¤J®g¥ú½u»P¨ä®g¥X½uªº¤Ï¦V©µ½u¥æ©ó¤@ÂIA¡A³q¹LA§@««ª½©ó¥D¥ú¶bªº««½u¥æ¥D¥ú¶b©óH1¡A¸ÓÂI§Y¬°¸Ó¨t²Îªº²Ä¤@¥DÂI¡C¦P¼Ë¡A±N¥¦æ©ó¥D¥ú¶bªº¤J®g½u»P§é®g½u©µªø½u¥æ©ó¤@ÂIB¡A¸ÓÂI»P¥D¥ú¶bªº««½u¥æ¥D¥ú¶b©óH2¡A¦¹ÂI§Y¬°¸Ó¨t²Îªº²Ä¤G¥DÂIH2¡A³q¹LHl¡BH2««ª½©ó¥D¶bªº¥±ºÙ¬°²Ä¤@¡B²Ä¤G¥D¥±(principal
plane)¨£¹Ï1-42¡C
±q¹Ï¤¤¥i¥H¬Ý¥X¡AµL½×¥ú½u¦b§é®g¨t²Î¤¤¸ô®|¬O«ç¼Ëªº¡A¦ý¦b®ÄªG¤W¬Û·í©ó¥u¦b¥D¥±¤Wµo¥Í§é®g¡C¦]¦¹§Ú̱N¢Öl§@¬°¤J®g½u°¼ªºìÂI¡A§Y¢Ô1¦Ü¢Öl¶¡ªº¶ZÂ÷§@¬°²Ä¤@µJ¶Zf1¡Fª«¨ì¢Ölªº¶ZÂ÷¬°ª«¶Zu¡F¦ÓH2§@¬°§é®g°¼ªºìÂI¡A§Y¢Ô2¦ÜH2ªº¶ZÂ÷¬°²Ä¤GµJ¶Zf2¡F¹³¨ì¢Ö2ªº¶ZÂ÷¬°¹³¶Zv¡C¦Ó³q¹L¤@Ó¥D·F±¤W¥ô¤@ÂIªº¥ú½u¤@©w³q¹L¥t¤@¥D¥±¤W¦ì¸m¬Û·íªº¹ïÀ³ÂI¡A¦pA»PA'¡AB»PB'¡C
(3)
¨âµ²ÂI¡@¦b¦@¶b¨t²Îªº¥D¥ú¶b¤WÁÙ¦s¦b¨âÓÂI¡ANl»PN2¡A¥H¥ô¦ó¨¤«×¦VNl¤J®gªº¥ú½u³£¥H¦P¤@¨¤«×¥ÑN2®g¥X¡CNl¤ÎN2¤À§OºÙ¬°²Ä¤@µ²ÂI©M²Ä¤Gµ²ÂI¡C¨£¹Ïl-42¤¤ªº3¡C
2.
«p³zÃ覨¹³¡@µL½×¦b¦h麽½ÆÂøªº¦@¶b©}¥ú¨t²Î¤¤¡A§t¦³¦h¤ÖÓ§é®g²y±(©Î³zÃè)©Î¥Ñ¥ô¦ó¤¶½èºc¦¨ªº½ÆÂø¥ú¾Ç¨t²Î¡A¥unª¾¹D¥DÂIH1¤ÎH2¡A¥DµJÂIFl¤ÎF2¡A¥H¤Îµ²ÂINl¤ÎN2¡A«h¥i¥Î§@¹Ïªk¨Ó¦¨¹³¡C®Ú¾Ú¥H¤U¤T±ø½uªº¥ô·N¨â±ø§Y¥i¨D¥Xª«ÂIªº¹³ÂI¡C
(1)
¥¦æ©ó¥D¥ú¶bªº¥ú½u¡A¦b²Ä¤G¥D¥±§é®g«á¹L²Ä¤GµJÂIF2¡F
(2)
³q¹L²Ä¤@µJÂIF1ªº¥ú½u¡A¦b²Ä¤@¥D¥±¤W§é®g«á¥¦æ©ó¥D¥ú¶b®g¥X¡F
(3)
¹Ï1-43¡@¥Î§@¹Ïªk¨D«p³zÃ覨¹³
(¤»)
¥ú¾Ç¨t²Îªº¹³®t
«e±©ÒÁ¿ªº¥ú¾Ç¨t²Îªº¦¨¹³°ÝÃD¡A§¡¬°ªñ¶b¥ú½uªº¦¨¹³¡A§Y¬°²z·Qªº¥ú¾Ç¦¨¹³¡A¦ý¦b¹ê»Ú¥ú¾Ç¨t²Î¤¤¤£¥i¯à¹F¨ì³o¤@²z½×n¨D¡A¦]¬°¥ú¾Ç¨t²Î¥»¨¦s¦bµÛºØºØ¹³®t¡A¤U±´N¥H¥ú¾Ç¹³®t¤¤³Ì±`¨£ªº³zÃè¹³®t¥[¥H»¡©ú¡C
1.
¦â¹³®t(chromatic aberration)¡@·í¤@§ô²V¦X¥ú(¥Õ¥ú)®g¦V³zÃ誺Ãä½t¡A¬Û·í©ó®g¦V¤@Ù±Ãè¡A¸gÙ±Ãè§é®g«á¡A¥i¨Ï¤£¦Pªiªøªº¥ú®g¥X®É§e¤ÀÂ÷ª¬ºA¡A§Î¦¨¦â´²¡F¦]³zÃèÃä½t¹ïªiªø¸ûµuªºµµ¦â¥ú½uªº§é®g«ü¼Æ¸û¤j¡A¦]¦¹¹ïµµ¥úªº§é®gµ{«×¸û±j¡A¨äµJÂI¶Z³zÃè³Ìªñ¡F¦Ó¬õ¦â¥úªºªiªø¸ûªø¡A§é®g«ü¼Æ¸û¤p¡A¦ÓµJÂI¶Z³zÃè¸û»·¡A¦Ó¨ä¾lÃC¦â¥úªºµJÂI«h¨Ì¦¸¦ì©óµµ¦â¥ú»P¬õ¦â¥ú¤§¶¡¡A³o¤@²{¶HºÙ¬°¦â¹³®t(¹Ï1-44)¡C
¦bÁ{§É¤W¡AµL´¹Åé²´¥Î¤j«×¼Æ¥Y³zÃèÁB¥¿®É¡A¯f¤H±`¶DÀ¹Ãè«á¬Ýª«Åé³£¦³±m¦âÃä¡A´N¬O¥Ñ©ó³zÃ誺¦â¹³®t©ÒP¡C
2.
²yµe¹³®t(spherical aberration)¡@³q¹L³zÃè©PÃ䪺¥ú½u¡A¦]¨ä¤J®g¨¤¸û¤j¡A©Ò¥H¨ä§é®g§@¥Î¤]¸û±j¡A¦]¦¹¡A¸g¹L³zÃè©PÃä§é®gªº¥ú½u¸ûªñ¶b¥ú½u§ó±µªñ©ó³zÃè§Î¦¨µJÂI¡A³oºØ²{¶HºÙ¬°³zÃ誺²y±¹³®t(¹Ï1-45)¡C¨ä¤¤F1¬°ªñ¶b¥ú½u³q¹L³zÃè«á©Ò§Î¦¨ªºµJÂI¡AF2¬°©PÃä¥ú½u³q¹L³zÃè«á©Ò§Î¦¨ªºµJÂI¡AFl»PF2¤§¶¡ªº¶ZÂ÷ªí©ú¦¹³zÃè¦s¦b²y±¹³®t¡C
3.
¹Ï1-46¡@±k§Î¹³®tªº§Î¦¨
±N¥H³q¹L¥ú¤ßªº¥ú½u¬°¨Ì¾Ú§@¤@»²§U¥ú¶b¡A¾aªñ»²§U¥ú¶bªº¥¦æ¥ú½u1³q¹L³zÃè«á¬Û¥æ©óÂIFl¡F»·Â÷»²§U¥ú¶bªº©PÃä¥ú½u2³q¹L³zÃè«á¬Û¥æ©ó¥t¤@ÂIF2¡A¦p¦bF2³B««ª½©ó¥ú¶b¸m¤@«Ì¨ÓÆ[¬Ý¥úªº¦¨¹³±¡ªp¡A«h¥i¨£¨ì¦p¹Ï1-47©Ò¥Ü¨º¼Ë§Î¦¨¤@Ó«D§¡µ¥·Ó®gªº±ù§Î¥ú´³¡A¦¹²{¶H§Y¬°±k§Î¹³®t©Ò¦¨ªº¹³¡C
4.
±×¥ú§ô´²¥ú――¹³´²²{¶H¡@·í¤@§ô±×¦æ¥ú½u®g¦V³zÃè¡A¨Ã³q¹L¤£§t¥ú¤ßªº³zÃ賡¤À©Òµo¥Íªº§é®g²{¶H¡A¨ä±¡§Î«ê¦pSturm¥úÀ@¤@¼Ë¡A¥¦æ¥ú½u©Ò¦¨ªº¹³¨Ã¤£§Î¦¨©ó¤@ÂI¡A¦Ó¬O§Î¦¨¨âÓ¤¬¬Û««ª½ªºµJ½u»Pµ{«×¤£¦P¡B¤è¦V¤£¤@ªº³\¦h¾ò¶ê§Î¹³¡A³o¼Ëªº¹³®tºÙ¬°¹³´²²{¶H(¹Ï1-48)¡C
5.
¹³³õÅs¦±(curvature of the field)¡@·í§Ú̳q¹L³zÃè¨ÓÆ[¹î¤@ªøªºª½½u®É¡A§Y¥i¨£¨ì¹³³õÅs¦±¡C¦¹ºØ²{¹³¬O¥Ñ©ó§@¬°ª«ªºªøª½½u¤W¦UÂI©Òµo®gªº¥ú½u¤¬¦V³zÃèªí±¶É±×ªº½t¬G¡A©Ò¥H©PÃ䳡¥ú½uªºµJÂI¸û¤¤¥¡¥ú½uªºµJÂI§óªñ©ó³zÃè¡C¦]¦¹¡A¦UÓµJÂI¤£¬O¦b¤@Ó¥±¤W¡A¦Ó¬O¦b¤@Ó¦±±¤W¡C±Nª«Åé¦U³¡©Ò¦¨µJÂI³s±µ°_¨Ó«á¡A«h¹³§eÅs¦±ªº¥~Æ[¡A³oºØ²{¶HºÙ¬°¹³³õÅs¦±(¹Ï1-49)¡C
³oºØ²{¶H¹ï²´ªº¦¨¹³¤£·|³y¦¨¼vÅT¡A¦]¬°¤H²´µøºô½¤¬OÅs¦±±¡C¹ïªñ¶b¥ú½u¦Ó¨¥¡A¹³³õÅs¦±¥i¥H©¿²¤¤£p¡C
¹Ï1-49¡@¹³³õÅs¦±²{¶H
6.
¹³·îÅÜ(distortion)¡Ð¹³§á¦±¡@·í³q¹L¤@°ª«×¥Y³zÃè¬Ý¤@¤è®æ§Îª«Åé®É¡A«h¤è®æªºÃä½t¦¨¥W§Î¤º³´¡F¦Ó³q¹L°ª«×¥W³zÃè®É¡A«h¤è®æªº¥|Ã䦨¥Y§Î¦V¥~¶©°_¡A³oºØ²{¶HºÙ¬°³zÃ誺¹³·îÅÜ¡C©M¨ä¥L¹³®t¤£¦P¡A¹³·îÅÜ»PµJÂIªº¾U§Q«×µLÃö¡A¦Ó¬O©M¹³ªº§Îª¬¦³Ãö¡C¦pªG³zÃ誺©ñ¤j²v¦b©Ò¦³³¡¤À³£¬Û¦Pªº¸Ü¡A³oÓª«ªº¹³¤~¬O¯u¹êªº¡C¦ý¬O¥ú½u·Uªñ³zÃ誺©PÃ䳡§é®g«áªº°¾¦V·U©úÅã¡C¦]¦¹¡A©ñ¤j²v¤£¬OùÚ©wªº¡A±q¦Ó²£¥Í¹³·îÅÜ(¹Ï1-50)¡C
|
||||||||||||||||||||||